In the last column, we introduced power semiconductors and improved their performance. We also mentioned that improving performance requires numerical measurements from several perspectives, which also requires test equipment to improve performance. In fact, not only the measurement of power semiconductors, the technology of numerical measurement itself has been attracting attention in recent years. The keyword is "IoT (Internet of Things)".

One of the major changes in measuring instruments is the change from analog to digital that has been advanced since the 1950s. For example, ammeters and voltmeters, which everyone used in science experiments in junior high school and high school, were an analog type with a needle that shows. However, in the analog type, it is required to read up to one-tenth of the finest scale, and you cannot read more detailed numbers. It may still be sufficient for using a science experiment in the school. But it is not enough in semiconductor design and its performance evaluation.

Therefore, digital measuring instruments have become mainstream at the development site, and not only display but also measurement parts are becoming digitalized. Information obtained by the sensor is digitized by A/D conversion as the basic operation. Many targets can be measured, and now digital values such as current, voltage, resistance, frequency, temperature, humidity, illuminance, pH, pressure, sound, distance, geomagnetism, acceleration, gyro, etc. are obtained.

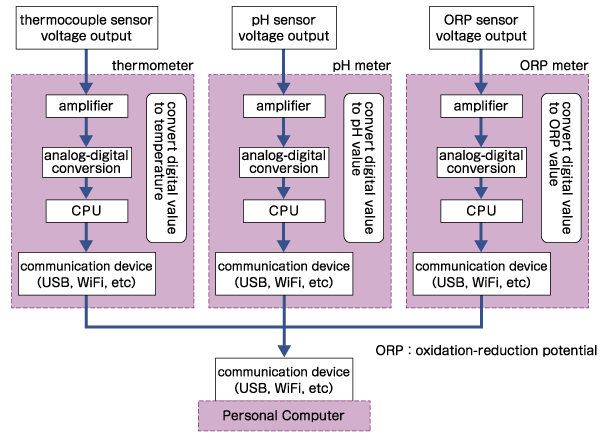
As pictured in the figure, the analog value acquired by each sensor is output as a voltage. After that, the signal (voltage) is amplified by an amplifier and A/D converted and then taken into a computer. The above figure gives an example of a sensor that is output as voltage. Image sensors used in Programmable Logic Controller (PLC) and digital cameras etc. A/D converts the (integrated) current value as the input value.

Recently, communication between sensors and computers, in some cases, tablets and smartphones, has often been performed via USB or wireless. Because it is difficult to lay cables for communication in the case of outdoor installation type sensors, such as digital instrument screens, especially, uploading of data by wireless is the mainstream. There are also cases where data is uploaded directly to the system built on the Internet.

Data acquisition by sensors has become possible because the size of the computer required to perform the same process is smaller than before. The advancement of SoC, System on Chip, technology is rapid, and a computer of a long time ago can be contained in a 1 cm square chip. This makes it possible to save enough power to operate even with solar cells and dry cells, and chips that can be used wirelessly can be bought for a thousand yen. In other words, the set of sensors and processing computers is cheap enough to be disposable.

Similarly, for wireless communication, since 3 G and 4 G mobile phone base stations are in place, data communication using mobile phone lines instead of wireless LANs has become mainstream. We also formulated Low Power Wide Area, LPWA, standards such as SIGFOX and LoRa, which enable communication with extremely low power consumption. Therefore, if hundreds of points of temperature, humidity, etc., can be converted into digital data by A/D conversion, it will be easy to send data directly to a server on the Internet through a cell phone line and process data aggregation.

The collected data is treated as big data, and the information processing according to the field such as social infrastructure monitoring, disaster prevention, and labor-saving of agriculture is performed and applied. IoT has been attracting attention in recent years as the use of such data has progressed.

Now, let's look at the change in the data value until such data is passed from the sensor to the computer. Here, the pH sensor is taken as an example.

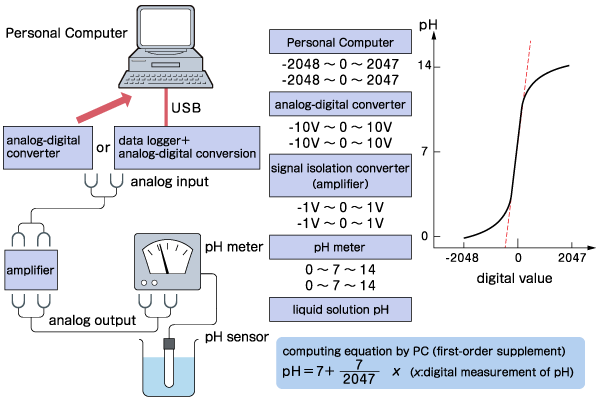
The value measured by the pH sensor converts a value between 0 and 14 when passed to the pH meter. The values at this time are still in analog form. There, it is once converted to a voltage in the range of -1 V to 1 V and sent to a signal isolation converter (amplifier). In the amplifier, it is amplified to -10V to 10V as the analog value. Then, A/D conversion is performed. As a result, the analog value of -10 V to 10 V is converted to a digital value of -2048 to 2047, which may be larger if it is a multiplier of 2, and then sent to a computer. Of course, you may convert it back to a digital value of 0-14 again before sending it to a computer. In any case, analog values are converted to voltages and then converted to digital values.

If the input is current, for example, in the programmable logic controller (PLC), the input value is often set to 0 to 20 mA of direct current, and this is often used by A/D conversion.

Well, Now, the flow of converting analog values to digital values should be known. However, when measuring these, the "resolution" becomes very important. It was explained earlier that it was converted from -2048 to 2047. Of course, a larger number may be used if it is a multiplier of two. The reason why the power of 2 is a multiplier is that the computer treats 1 bit, which is a unit of information "0 or 1", as a unit of basic information. So, the number 2048 to be called "11 bit" mentioned above is 2 to the 11th power. Furthermore, by adding one bit (0 for a positive number, 1 for a negative number) to determine whether it is positive or negative at the beginning and making it 12 bits, if "111111111111", then "-2048" and "011111111111" can be written as "2047".

The fact that this number is large means that the value of -10 V to 10 V can be finely resolved. This fineness is called "resolution".

Recently, measuring instruments have increasingly been required to obtain more accurate measurement values and errors. For this reason, higher resolutions enable more precise measurement, so it is an important development requirement to decide how much resolution to aim for in production. Also, the setting of resolution is very important because the testing side cannot select the correct measurement equipment unless the required resolution is set firmly.

The figure below is a comparison of low and high resolution.

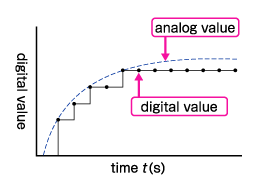
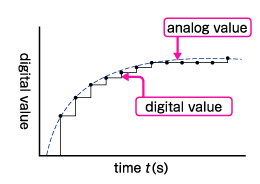
This is a graph of analog value over time. As can be seen, when the fluctuation of the leftmost analog value is converted to a digital value, the graph at the right end, high resolution, produces a value closer to the analog value than the graph in the middle, low resolution. Therefore, the higher the resolution, the more accurate measurement results can be displayed.

Also, the time on the horizontal axis is the same. By outputting data in as short a time as possible, time changes can be measured in detail. In this case, the processing speed of the computer and A/D conversion board has been improved, so it is possible to measure in a much shorter time compared to 10 years ago and 20 years ago.

However, it doesn't mean that you should simply make it shorter. When the original input to be measured is small, a short time will result in large deviations or errors in the measured value. For example, you consider taking a picture in the darkroom. Then, the amount of light coming into the sensor is few, so taking a picture in a short amount of time will result in an overall rough picture. In other words, when the amount of the object to be measured is originally small, when there are only ten inputs on average over a fixed time, if there are 11 inputs occasionally, the value will be 1.1 times larger. If you have 10000 inputs, you can see that it is a good level that you don't care about even at 10001.

Therefore, it is necessary to carefully consider the measurement timing and the integration (accumulation) time used for measurement. It is important to consider what design is required and what pattern of measurement may be possible when measuring voltage and current values, measuring switching timing, measuring resistance, measuring the operating environment temperature, etc.